That is indeed a convoluted title, but it's the bare minimum I could think of to really describe the theme of this page/post/article. The secondary reason why the title convoluted is just that it has more words and punctuations than what is generally accepted for these sorts of posts.
Now, the primary reason is that it's not nice on your working memory:
"Working Memory Capacity is the ability to hold raw information in immediate awareness so that that it can be manipulated and transformed into a more useful form"
(Schneider & McGrew, 2012).
For instance, it's probably easy for you to tell what this means:
Almost just as easy to say:
And it'll probably start to not be so obvious at:
And perhaps impossibly hard for any neurotypical to grasp:
Surely, what's missing in the bottom right is another red ball, so the answer is C.
Now just think about how you know that is the answer and not anything else. It's simply the most plausible answer by any reasonable standards, and definitely, the right answer taking into account that someone designed this. You know this because it's a pattern and a straight forward one at that.
Now think about this one:

There are variables:
1) Green plus sign
2) Pink square
3) Blue plus sign
4) Yellow cross
5) Red diamond-shaped things at the corners of a square (?)
6) Pink circle around things
If you write it down like that, it's straight forward that there two missing: (6) and (3):

And that's indeed the right answer.
You're not allowed to paper either on the intelligence-quotient tests, as that'd be a sort of cheating--Intelligence is highly dependent on working memory.
Anyway, eventually, these tests no longer make it possible to solve by counting and surface-pattern identification. You need to understand the underlying mechanism; the logic; what is happening.

This is an easy example of one which is easy to visualize the silver squares going up in each column and to the right in each row, hence the answer is (logically) A.
Here's where that starts to fail you:

You can't count or keep track of variables to solve it. You need to understand that it has a logic behind it, that there is a meaningful "cause", and not just a random fact/rule like the previous two.
This is just like that 'negation-negation-statement' in both English and math; there is the understanding of what's happening vs being able to extract out a rule/pattern/law to be used as a tool to solve something without truly grasping it.
In this case, a ball inside the circle represents a negative and so outside represents a positive. The first two in each row "add up" to make the third.
First row: -1 -1 = -2
Second row: -1 +3 = 2
Third row: -2 + 2 = 0
So the anger is G.
Let's just do two more. Here's another example of one that you can somewhat easily solve by counting:

For each one there is a vertical, horizontal and diagonal.
For each one there are 1, 2 and 3 sticks.
What's missing? 1 stick and vertical:

Another way you can start to think about it is this:
For each row, you can see that the sticks are going from 1, 2 to 3.
In the next row, it is the SAME story but now it shifted to the right.
You can also see that the order of horizontal - diagonal - vertical stays.
Once you understand this logic, the answer is obvious, and no counting is needed.
Lastly, try to think about this one:

You can't solve it by counting unless you have a pen and quite a bit of space on paper.
The logic is that there are three separate lines, tied at one end by each of the balls in the second row. They're simply twisting clockwise.
So the answer is:


The unit shape, inferred from the sides are 3 by 4, would be 1 cm.
If the sides were 3.5 by 4, then the unit shape would have to be 0.5cm.
If the sides were 3.1 by 3.5, can you tell what the unit shape would have to be?
0.1, as it is the biggest x-by-x square you could get to fill up a 3.1 by 3.5 larger square. The area is (again, by definition) how many of these are required.
Simply, it's just the product of the two sides; 3.1m * 3.5m = 10.85 m^2
Note that the answer being "10.85" makes absolutely no sense if you understand what area is. The answer is how many UNIT SQUARES (in this case, 0.1-by-0.1 metres unit squares) are needed to fit the criteria in the DEFINITION.
D E F I N I T I O N.
That's where it stops downward, but not upward;

The area of a triangle can be understood to be half of the area of that rectangle. The formula "A = 1/2 b*h" is just from this logic, and so is the formula for every area and volume; it can all be proved and understood logically, starting from the definition of area and volume.
Once we go down this deep, even in the case of calculus (power rule), we stop at definitions and axioms:
For example, the axioms of algebra:
Source: https://www.aaamath.com/ac11.htm
The term has a central theme across different fields of study, however, it's defined slightly different:
In classic philosophy: "Any statement that is evident and well-established to the degree it is accepted without disagreements"
In modern logic: Any statement (which is any sentence with a truth value; it's either true or false), called a premise in logic, used as a starting point to reason from.
In mathematics:
I think that's what human thoughts are about; we put a set of constraints on the world and play from those rules. Mathematical theories, such as Euclidean geometry, are based on a set of assumptions. Albeit not matching reality (such as spacetime not curving), they work for a level of resolution most common to us.
This brings us to the idea that 'truth' and 'myths' have a bridge. In Homo Deus, Yuval talks about how oftentimes it's Reality that has to submit to our myths, like when the Europeans divided the African continents falsely but people had to change their ways and the land was restructured. Furthermore, religion is a great example of something not very 'objective' or 'scientific' and yet, the tools of knowledge work for us.
But what about objectively-derived models?
If we look at Newtonian physics, we have a fairly objective model with wrong but workable assumptions. The Einsteinian model goes a step deeper, but it will most certainly be looked down on in the future. Yet, it's still quite obviously different from religious myths.
Let's distinguish the two then:
-We ought to consider everyone's feelings
-The heroe myth, considered in a positive light.
-Kinematics
-Special Relativity
-Chemistry
We can compare our "moral theories" to a logical conclusion;
if a=b and a=c, then b=c
if humans have intrinsic value and John is a human, John's life has to be valued; no killing, etc.
Relates to Feynman's "why":
He explains that you can't just ask "WHY are these two magnets attracting?"
His analogy is by asking "why did mary slip off the ice?"
Some would be satisfied with "she was rushing to the hospital to see her husband and it was freezing outside".
You could also say "because ice is slippery". Why? "Because the contraction of ice on your feet creates a laywer of water between you two, thus slippery". Why? "Because of the liquid nature of water, so there's no more friction between her shoes and the ice"....
Or:
Why wen to hospital cuz husband was sick?
We all understand that wives tend to love their husbands and that when people are sick they go to the hospital. we also understand that you want to be near someone you love when they're sick for support. If you ask WHY, you go into evolution.
So, Mary slipper off the ice because of chemistry/physics? Evolution/biology? Psychology? What suffices? What is ENOUGH? Why is x enough?
Relates to Peterson's "thing in itself":
I'm in
Now, the primary reason is that it's not nice on your working memory:
"Working Memory Capacity is the ability to hold raw information in immediate awareness so that that it can be manipulated and transformed into a more useful form"
(Schneider & McGrew, 2012).
For instance, it's probably easy for you to tell what this means:
- (i) Grab the cup.
Almost just as easy to say:
- (ii) Don't grab the cup
And it'll probably start to not be so obvious at:
- (iii) Don't not grab the cup.
And perhaps impossibly hard for any neurotypical to grasp:
- (iv) Don't not not not not not not not grab the cup.
This would be the equivalent to the sort of jokes that kids make like "I know you think that I think that you think that I want to throw you a surprise party!"
Most people would be uncomfortable after 3-4 steps in these sort of things.
It's the same reason that postcodes, phone numbers, etc, are divided into 3-4 sections:
Ph: 0411 111 111
Postcode: 2222
Or any sort of way that numbers get organized to make it good enough for people to process.
But what is that reason?
"Several other factors affect a person's measured span, and therefore it is difficult to pin down the capacity of short-term or working memory to a number of chunks. Nonetheless, Cowan proposed that working memory has a capacity of about four chunks in young adults (and fewer in children and old adults)."
From: "The magical number 4 in short-term memory: A reconsideration of mental storage capacity"
https://www.cambridge.org/core/journals/behavioral-and-brain-sciences/article/magical-number-4-in-shortterm-memory-a-reconsideration-of-mental-storage-capacity/44023F1147D4A1D44BDC0AD226838496
https://www.cambridge.org/core/journals/behavioral-and-brain-sciences/article/magical-number-4-in-shortterm-memory-a-reconsideration-of-mental-storage-capacity/44023F1147D4A1D44BDC0AD226838496
So that's it: our working memory starts to fail us past four 1-bit variables.
(1) A 1-bit variable would be "red".
(2) A 2-bit variable would be "red truck".
(3) A 4-bit variable would be "100 km/hr, red, Mercedes truck".
Think about this, though: It would be easier to think about that 4-bit variable "100 km/hr, red, Mercedes truck" and another 4-bit variable (say) "blue, pregnant, sleeping whale", which makes it a total of 8-bit, than it would be to think about 5 or more separate ideas at once, making it 5-bits.
This should give you an idea of the complexity of this sort of thing, but hopefully enough for you to grasp the topic and relate this to the previous and subsequent ideas.
This should give you an idea of the complexity of this sort of thing, but hopefully enough for you to grasp the topic and relate this to the previous and subsequent ideas.
Now let's go back to the cup examples (iii) and (iv).
(iii) is short enough for you to actually grasp it in your mind, i.e., enough for your working memory to hold and 'you' to visualize how it just... makes sense. It's clear that (iii) means to NOT do the act of "not grabbing", which means to just grab.
Makes you think about the meaning of the word grasp, doesn't it?
We might start to think of our working memory as our intellectual hands for abstract objects:
"It is widely supposed that every entity falls into one of two categories: Some are concrete; the rest abstract.
...it is universally acknowledged that numbers and the other objects of pure mathematics are abstract [if we agree numbers exist], whereas rocks and trees and human beings are concrete. Some clear cases of abstracta are classes, propositions, concepts, the letter ‘A’, and [some famous poem]. Some clear cases of concreta are stars, protons, electromagnetic fields, the chalk tokens of the letter ‘A’ written on a certain blackboard, and [a paper with some famous poem]."
...it is universally acknowledged that numbers and the other objects of pure mathematics are abstract [if we agree numbers exist], whereas rocks and trees and human beings are concrete. Some clear cases of abstracta are classes, propositions, concepts, the letter ‘A’, and [some famous poem]. Some clear cases of concreta are stars, protons, electromagnetic fields, the chalk tokens of the letter ‘A’ written on a certain blackboard, and [a paper with some famous poem]."
(Stanford Encyclopedia of Philosophy, 2001)
Now look at (iv). You might or might not have figured out what you're supposed to do (grab or not grab the cup), but even for anyone who figured it out, did you have all the words in your head and understood how they all interact to form the final meaning of the sentence? Unless you're an outlier for working memory capacity, you certainly didn't.
Here's a way we can figure it out without truly grasping it:
Do grab the cup = +Grab
Do not grab the cup = -Grab
Do not not grab the cup = +Grab
Do not not not grab the cup = -Grab
....
See a pattern? It's flipping back and forth from positive to negative, i.e., from grabbing the cup to not grabbing the cup.
We can find the answer by seeing how many "nots" there are, as they'll keep cancelling each other out.
In our (iv) example (including the "not" in "Don't") we have 8 "nots".
Up to the 7th "not", it was to NOT touch the cup in the end. Adding the 8th "not", it means to not do that, i.e., to actually touch the cup.
The 'rule' we can infer from this pattern is that for an odd number of "nots" we end up with a negative, and for an even number of "nots" we end up with a positive.
This is just like the rules in math:
And so, for exponents, when we have e.g.
(-1)×(-1), which is (-1) ², we know the answer is +1
If we multiply that by -1:
(-1)×(-1)×(-1), which is (-1)³
We have -1
(-1)×(-1)×(-1), which is (-1)³
We have -1
And the odd/even rules are just memorized, without most people having a grasp of the underlying logic.
This is the case for a myriad of things in math which you can start to research on your own as I could write a book with examples.
Moving on, we can also get a better idea of this from some puzzles with patterns.
Let's with the easiest possible one:
Let's with the easiest possible one:
Surely, what's missing in the bottom right is another red ball, so the answer is C.
Now just think about how you know that is the answer and not anything else. It's simply the most plausible answer by any reasonable standards, and definitely, the right answer taking into account that someone designed this. You know this because it's a pattern and a straight forward one at that.
Now think about this one:

There are variables:
1) Green plus sign
2) Pink square
3) Blue plus sign
4) Yellow cross
5) Red diamond-shaped things at the corners of a square (?)
6) Pink circle around things
If you write it down like that, it's straight forward that there two missing: (6) and (3):

And that's indeed the right answer.
You're not allowed to paper either on the intelligence-quotient tests, as that'd be a sort of cheating--Intelligence is highly dependent on working memory.
Anyway, eventually, these tests no longer make it possible to solve by counting and surface-pattern identification. You need to understand the underlying mechanism; the logic; what is happening.

This is an easy example of one which is easy to visualize the silver squares going up in each column and to the right in each row, hence the answer is (logically) A.
Here's where that starts to fail you:

You can't count or keep track of variables to solve it. You need to understand that it has a logic behind it, that there is a meaningful "cause", and not just a random fact/rule like the previous two.
This is just like that 'negation-negation-statement' in both English and math; there is the understanding of what's happening vs being able to extract out a rule/pattern/law to be used as a tool to solve something without truly grasping it.
In this case, a ball inside the circle represents a negative and so outside represents a positive. The first two in each row "add up" to make the third.
First row: -1 -1 = -2
Second row: -1 +3 = 2
Third row: -2 + 2 = 0
So the anger is G.
Let's just do two more. Here's another example of one that you can somewhat easily solve by counting:

For each one there is a vertical, horizontal and diagonal.
For each one there are 1, 2 and 3 sticks.
What's missing? 1 stick and vertical:

Another way you can start to think about it is this:
For each row, you can see that the sticks are going from 1, 2 to 3.
In the next row, it is the SAME story but now it shifted to the right.
You can also see that the order of horizontal - diagonal - vertical stays.
Once you understand this logic, the answer is obvious, and no counting is needed.
Lastly, try to think about this one:

You can't solve it by counting unless you have a pen and quite a bit of space on paper.
The logic is that there are three separate lines, tied at one end by each of the balls in the second row. They're simply twisting clockwise.
So the answer is:

(The middle one, which is diagonal, twisted clockwise and is now horizontal. The two lines on the side also twisted clockwise but had to go 180° to the next red ball)
Now I'd like to talk about how this applies to math and physics. However, it will just take too much time to explain what is everywhere on the web: the derivation and/or proof of any sort of rule, really!
For those at calculus level: I highly recommend thinking about the "power rule" versus "differentiation from first principles. I always like Khan Academy for math explanations, so here is the Salman Khan himself in a 2007 video:
https://www.youtube.com/watch?v=rAof9Ld5sOg
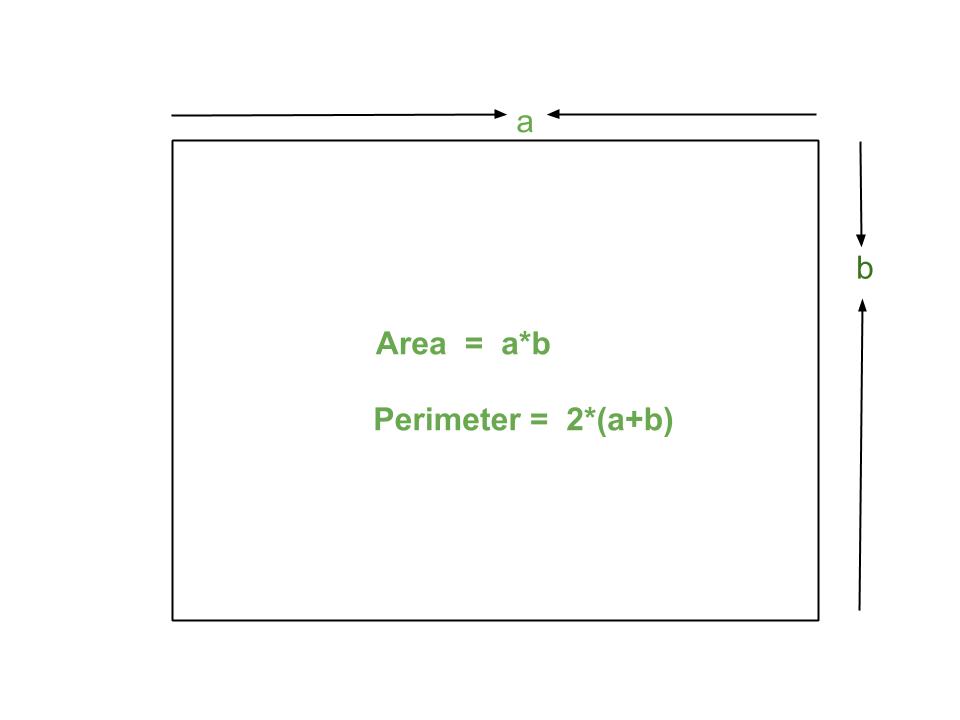
Now that we understand the concept, let's explore it as deep as you can go. Let's start by thinking what the area of this rectangle is:
But why is it that? What is the underlying logic? As far as I can tell, it is not some "property-of-the-universe", nor some logical necessity, but a human constructs from the definition:
Now I'd like to talk about how this applies to math and physics. However, it will just take too much time to explain what is everywhere on the web: the derivation and/or proof of any sort of rule, really!
For those at calculus level: I highly recommend thinking about the "power rule" versus "differentiation from first principles. I always like Khan Academy for math explanations, so here is the Salman Khan himself in a 2007 video:
https://www.youtube.com/watch?v=rAof9Ld5sOg
Now that we understand the concept, let's explore it as deep as you can go. Let's start by thinking what the area of this rectangle is:
But why is it that? What is the underlying logic? As far as I can tell, it is not some "property-of-the-universe", nor some logical necessity, but a human constructs from the definition:
"The area of a plane figure is the number of unit shapes required to cover it up completely with no overlapping or going over the edges."
You can think of a "unit shape" like this:
The unit shape, inferred from the sides are 3 by 4, would be 1 cm.
If the sides were 3.5 by 4, then the unit shape would have to be 0.5cm.
If the sides were 3.1 by 3.5, can you tell what the unit shape would have to be?
0.1, as it is the biggest x-by-x square you could get to fill up a 3.1 by 3.5 larger square. The area is (again, by definition) how many of these are required.
Simply, it's just the product of the two sides; 3.1m * 3.5m = 10.85 m^2
Note that the answer being "10.85" makes absolutely no sense if you understand what area is. The answer is how many UNIT SQUARES (in this case, 0.1-by-0.1 metres unit squares) are needed to fit the criteria in the DEFINITION.
D E F I N I T I O N.
That's where it stops downward, but not upward;
The area of a triangle can be understood to be half of the area of that rectangle. The formula "A = 1/2 b*h" is just from this logic, and so is the formula for every area and volume; it can all be proved and understood logically, starting from the definition of area and volume.
Once we go down this deep, even in the case of calculus (power rule), we stop at definitions and axioms:
For example, the axioms of algebra:
Source: https://www.aaamath.com/ac11.htm
The term has a central theme across different fields of study, however, it's defined slightly different:
In classic philosophy: "Any statement that is evident and well-established to the degree it is accepted without disagreements"
In modern logic: Any statement (which is any sentence with a truth value; it's either true or false), called a premise in logic, used as a starting point to reason from.
In mathematics:
a) Logical axioms: Can be thought of like the one in classic philosophy; they're taken to be true within the system of logic they define. E.g., the statement (A & B) implies B.
b) Non-logical axioms: Probably closer to be thought of as "definitions", i.e. what I mentioned about a 'human construct. These are, e.g., a + b = b+ a in algebra. They're part of different mathematical theories, such as algebra.
I think that's what human thoughts are about; we put a set of constraints on the world and play from those rules. Mathematical theories, such as Euclidean geometry, are based on a set of assumptions. Albeit not matching reality (such as spacetime not curving), they work for a level of resolution most common to us.
This brings us to the idea that 'truth' and 'myths' have a bridge. In Homo Deus, Yuval talks about how oftentimes it's Reality that has to submit to our myths, like when the Europeans divided the African continents falsely but people had to change their ways and the land was restructured. Furthermore, religion is a great example of something not very 'objective' or 'scientific' and yet, the tools of knowledge work for us.
But what about objectively-derived models?
If we look at Newtonian physics, we have a fairly objective model with wrong but workable assumptions. The Einsteinian model goes a step deeper, but it will most certainly be looked down on in the future. Yet, it's still quite obviously different from religious myths.
Let's distinguish the two then:
Examples of myths:
-Human life has intrinsic meaning-We ought to consider everyone's feelings
-The heroe myth, considered in a positive light.
Examples of theories:
-A^2 + B^2 = C^2-Kinematics
-Special Relativity
-Chemistry
We can compare our "moral theories" to a logical conclusion;
if a=b and a=c, then b=c
if humans have intrinsic value and John is a human, John's life has to be valued; no killing, etc.
Think about the number of things you see some data from; some consequence of; perhaps even some pattern from; yet have no idea of the underlying mechanism.
Mechanistic vs probabilistic evidence:
I have to study this further, but the paper clearly explains how we have explanations AND correlational data. There is only one type of cause; multi-causal theories fail.
There is "hypothesis-to-theory" by acquiring measurements and THEN reasoning.
Empirical vs reasoned knowledge
We must distinguish these two.
When I do the pendulum experiment, I can infer that I will have something roughly circular. To prove, logically, that the dropping-height doesn't affect period and THEN test it. This is theory-to-hypothesis.
-Just a "rule" to remember for the other one
Next, we can ask:
Just how much is useful?
In math, sometimes it's enough to memorize/understanding some system to which you can use as a tool, without going down to conceptually holding an understanding of it's own underlying functionality.-Calculating solar system from heliocentric vs not
-Can it ever end?
-The thing in itself; the useful (where to look, heuristics) is related to how we can shape our perception.
-The working memory does limit how much you can see. However, building up of concepts from 4 working--->long term and eventually larger picture?
-Deleuze's Rhizome:
I once got in a deep conversation with my best friend while we were hiking. We were talking about what it is to "love" or "feel bad". We kept going further and further into the rabbit hole, when we realized that there's a "difference" between "the brain is processing x chemical as a reaction to y object" vs "self/brain feels love for other-self/brain" and how there was a 'jump' between the cold former and warm latter.Relates to Feynman's "why":
He explains that you can't just ask "WHY are these two magnets attracting?"
His analogy is by asking "why did mary slip off the ice?"
Some would be satisfied with "she was rushing to the hospital to see her husband and it was freezing outside".
You could also say "because ice is slippery". Why? "Because the contraction of ice on your feet creates a laywer of water between you two, thus slippery". Why? "Because of the liquid nature of water, so there's no more friction between her shoes and the ice"....
Or:
Why wen to hospital cuz husband was sick?
We all understand that wives tend to love their husbands and that when people are sick they go to the hospital. we also understand that you want to be near someone you love when they're sick for support. If you ask WHY, you go into evolution.
So, Mary slipper off the ice because of chemistry/physics? Evolution/biology? Psychology? What suffices? What is ENOUGH? Why is x enough?
I'm in