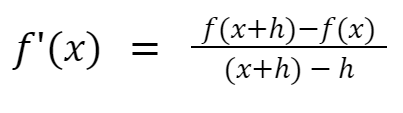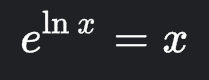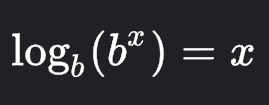Sky Castle

--What if the DISTANCE always EQUALED the velocity (in an esponential function)?

Suppose we wanted to graph my distance from point A when I am standing still at point B:

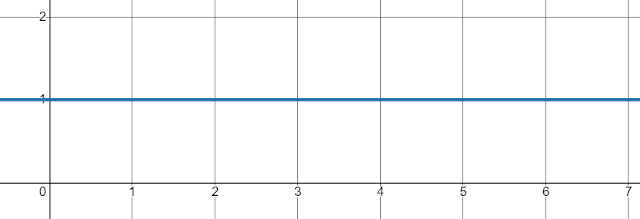
Note that A and B are 5 metres apart.

Suppose we drew a graph with the y-axis measuring distance (in metres) and the x-axis measuring time (in seconds). Therefore, since I'm not moving, my distance-time graph will be as such:

The y-axis is a straight, unchanging line at y=5 (i.e., 5 metres from point A) because I am standing still.

Imagine a second scenario where I began at point A and began moving (at a consistent rate) in the direction of point B (i.e., left to right on the road). In that case, my distance from point A is changing for every second that goes by. We say I am moving at a constant speed.

Suppose that speed is exactly 1 metre for every second; 1m/s:

Now my distance-time graph has a slope: the rate of change of distance is exactly 1 metre up by every second that goes by.

Speed, or velocity, is defined as the rate of change in distance per time. Therefore, our velocity is "1", in the units "m/s".

Let us then graph our velocity:

This velocity-time graph (i.e., the rate of change of velocity with respect to time) has a straight line because our speed isn't changing; only our distance is changing. Our speed is a constant 1m/s.

Therefore, note that when we were not moving (that is, when we were standing still at point A), our speed was zero.

Now, the same way that our distance from A increases as we move, our speed itself can also change. We call this change in speed an acceleration. That is when you put the foot down on the pedal of the car and your velocity steadily goes up:

If the speed was pointing steadily at (say) 40, then we are not accelerating: our speed is constant. It is only when the speed meter is going up--it's moving--that acceleration is happening.

Suppose our speed is increasing by 2m/s every second that goes by. This is a constant increase of 2, thus an acceleration of 2:

a= 2 2 2 2

t= 1 2 3 4

However, our velocity:

v=0 2 4 6 8 10

t= 0 1 2 3 4 5

Distance is then going to be a bit more complicated. It's not longer increasingly linearly, because the rate at which we are moving is itself increasing.

d=0 1 4 9 16 25

t=0 1 2 3 4 5

The problem at finding our rate of change of distance is that now the graph is CURVED; so it's steaper at some points.

With differentiation, we can zoom in infinitely to find the exact slope at any point.

With the integral, we can look at a velocity-time graph and find the distance covered (area under the curve, but ALSO can be thought of as the distance that'd have that slope; i.e. just finding a point in the d-t graph).

Integral: going from acceleration-->velocity-->distance.

If we think of the distance covered as the velocity at any time point multiplied by the time covered, if we add up all the little distances (v*t), we find the area under the graph.

Derive: distance-->velocity-->acceleration.

-----------------Logical, intuitive explanation for both-----------